Let’s get Lean
(warning: I’m not trying here to explain something to folks outside computer science, but more summarize something awesome I’m learning that is changing how I write code)
As software systems grow increasingly complex and automated, ensuring correctness becomes a monumental challenge. In a future of automatically generated code, certainty is both elusive and critical. Enter Lean, a modern interactive theorem prover designed to help you reason rigorously about your code, verify its correctness, and even prove mathematical theorems. A long term research thread of mine is to make these tools increasingly useful with the goal of building stuff faster while dramatically increasing security.
Lean is a functional programming language and interactive theorem prover created by Leonardo de Moura at Microsoft Research in 2013, now an open-source project hosted on GitHub. It facilitates writing correct and maintainable code by focusing on types and functions, enabling users to concentrate on problem-solving rather than implementation details. Lean boasts features such as type inference, first-class functions, dependent types, pattern matching, extensible syntax, hygienic macros, type classes, metaprogramming, and multithreading. It also allows verification by proving properties about functions within the language itself. Lean 4 is the latest version, supported by the active Lean community and the extensive mathematical library Mathlib. Additionally, the Lean FRO nonprofit was founded in 2023 to enhance Lean’s scalability, usability, and proof automation capabilities.
Lean is a formal proof assistant—a tool that allows you to write mathematical proofs or verify software formally. It merges powerful logical foundations with ease of use, making formal verification more approachable than ever before. It’s fully integrated with visual studio.
This matters because formal verification with Lean significantly improves software reliability, reducing bugs and enhancing safety in critical sectors such as aerospace, finance, and healthcare. Lean’s rigorous approach provides exceptional precision, enabling detection of subtle errors that traditional testing often overlooks. Additionally, Lean offers profound mathematical insights, empowering mathematicians to formally confirm intricate proofs common in advanced mathematics. If fully understanding the logic of advanced math isn’t the most powerful application of AI, I don’t know what is.
Real Example
What does the most simple lean program look like?
. ├── Hello │ └── Basic.lean ├── Hello.lean ├── Main.lean ├── README.md ├── lake-manifest.json ├── lakefile.toml └── lean-toolchain
In Hello/Basic.lean, we define a basic greeting:
def hello := "world"
The Hello.lean file serves as the root module, importing Hello.Basic:
import Hello.BasicThe Main.lean file combines these elements and includes a formal proof:
import Hello
def main : IO Unit :=
IO.println s!"Hello, {hello}!"
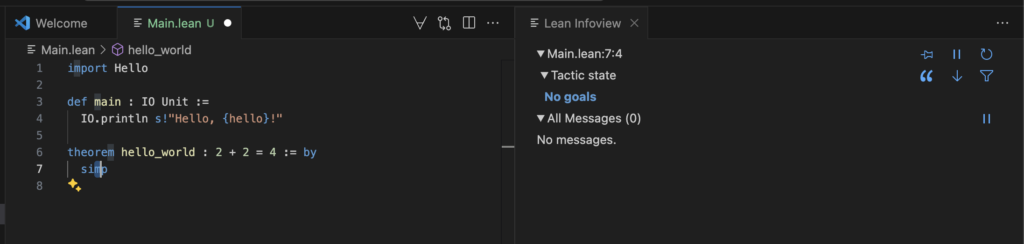
theorem hello_world : 2 + 2 = 4 := by
simpHere, the main function prints a greeting, while the hello_world theorem demonstrates Lean’s capability to formally verify that 2 + 2 equals 4 using the simp tactic.
In Lean 4, the simp tactic is a powerful tool used to simplify goals and hypotheses by applying a collection of simplification lemmas, known as simp lemmas. These lemmas are tagged with the @[simp] attribute and are designed to rewrite expressions into simpler or more canonical forms. When invoked, simp traverses the goal or hypothesis, applying applicable simp lemmas to transform the expression step by step. For example, in proving the theorem 2 + 2 = 4, the simp tactic automatically simplifies the left-hand side to match the right-hand side, effectively completing the proof without manual intervention. This automation makes simp an essential tactic for streamlining proofs and reducing boilerplate in formal verification.
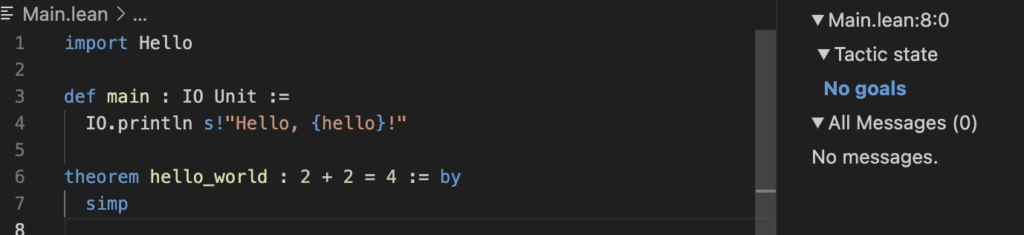
By running lake build, Lean compiles the project and verifies the theorem. If the theorem is incorrect or the proof is invalid, Lean will provide an error, ensuring that only mathematically sound code is accepted.
This approach to software development, where code correctness is mathematically guaranteed, is especially valuable in critical systems where reliability is non-negotiable. Lean 4 empowers developers to write code that is not only functional but also formally verified, bridging the gap between programming and mathematical proof.
At this point, you are probably wondering, what Lean can really do. Every human knows 2 + 2 = 4. So let’s do something real with a real proof by induction.
-- a more interesting proof: ∀ a b, a + b = b + a
theorem add_comm (a b : Nat) : a + b = b + a := by
induction a with
| zero =>
-- 0 + b = b + 0 reduces to b = b
simp
| succ a ih =>
-- (a+1) + b = (b + a) + 1 by IH, then simp finishes
simp [ih]In this example, Lean isn’t merely checking a single arithmetic equation; it’s proving that addition on the natural numbers is commutative in full generality. By invoking the induction tactic on \(a\), Lean first establishes the base case where \(a = 0\)—showing \( + b = b + 0\) reduces to the trivial identity \(b = b\)—and then handles the inductive step, assuming \(a + b = b + a\) to prove \((a + 1) + b = b + (a + 1)\). In each case, the simp tactic automatically applies the appropriate lemmas about Nat addition to simplify both sides of the equation to the same form. Finally, when you run lake build, Lean silently compiles your code and verifies both the simple fact \(2 + 2 = 4\) and the full commutativity theorem; if any part of the proof were flawed, the build would fail, ensuring that only completely correct mathematics makes it into your code.
You can continue this to prove other properties of math.
import Hello
def main : IO Unit := do
IO.println s!"Hello, {hello}!"
IO.println "All proofs have been verified by Lean!"
-- trivial fact: definitionally true
theorem hello_world : 2 + 2 = 4 := by
rfl
-- use core lemmas directly
theorem add_comm (a b : Nat) : a + b = b + a := by
exact Nat.add_comm a b
theorem mul_add (a b c : Nat) : a * (b + c) = a * b + a * c := by
exact Nat.mul_add a b cFor the more substantial theorems, we use the exact tactic to invoke core library lemmas directly: Nat.add_comm proves commutativity of addition \((a + b = b + a)\), and Nat.mul_add proves distributivity of multiplication over addition \((a * (b + c) = a * b + a * c)\). By relying on these already‑proven lemmas, Lean’s compiler verifies each theorem at build time—any failure in these proofs will cause lake build to error out.
Ok, so proving the basic properties of math is super cool, but how exactly is this useful? Below is an example of a “real‑world” optimization—rewriting a naive, non‑tail‑recursive summation over a list into a tail‑recursive loop—and formally verifying that the optimized version is equivalent to the original. This kind of proof is exactly what you’d need to trust that your performance tweaks haven’t changed the meaning of your code.
In embedded systems, optimization matters. The code below demonstrates how Lean can formally verify that a tail-recursive optimization is functionally equivalent to its naive counterpart—a task that’s often error-prone when done manually in traditional languages like C. The function sum is a simple, natural recursive definition that adds up all the elements of a list. It’s clear and expressive but not stack-safe for large inputs due to its non-tail-recursive form. To improve performance, we define sumAcc, which uses an explicit accumulator and a tail-recursive helper function to avoid deep call stacks. The theorem sum_correct proves that for any list of natural numbers, sum xs = sumAcc xs. This is mathematically interesting because it confirms—using structural induction and algebraic reasoning—that the transformation preserves meaning across all inputs, not just for a few test cases. In systems programming terms, this is like formally proving that a loop unrolling or inlining optimization didn’t introduce a subtle bug—a capability that’s increasingly essential as code becomes more complex and performance-critical.
import Hello
import Std.Data.List.Basic
open Std
def main : IO Unit := do
IO.println s!"Hello, {hello}!"
IO.println "All proofs have been verified by Lean!"
-- naive, non‑tail‑recursive sum
def sum : List Nat → Nat
| [] => 0
| x :: xs => x + sum xs
-- optimized, tail‑recursive sum using an accumulator
def sumAcc (xs : List Nat) : Nat :=
let rec go (ys : List Nat) (acc : Nat) : Nat :=
match ys with
| [] => acc
| y :: ys => go ys (acc + y)
go xs 0
-- proof that the optimized version agrees with the naive one
theorem sum_correct (xs : List Nat) : sum xs = sumAcc xs := by
induction xs with
| nil =>
-- sum [] = 0, sumAcc [] = go [] 0 = 0
rfl
| cons x xs ih =>
-- sum (x :: xs) = x + sum xs
-- sumAcc (x :: xs) = go (x :: xs) 0 = go xs (0 + x)
-- we simplify and then apply the inductive hypothesis
simp [sum, sumAcc]
-- now we have: x + sum xs = sumAcc xs + x
-- but sumAcc xs = sum xs by ih, and addition is commutative
rw [ih]
If we were to sit down and do the math of this, it’s not straightforward:
We define two functions to compute the sum of a list of natural numbers. The first is a simple recursive version:
$$ \text{sum}([]) = 0 $$ $$ \text{sum}(x :: xs) = x + \text{sum}(xs) $$The second is an optimized version using a tail-recursive helper function with an accumulator:
$$ \text{go}([], acc) = acc $$ $$ \text{go}(y :: ys, acc) = \text{go}(ys, acc + y) $$ $$ \text{sumAcc}(xs) = \text{go}(xs, 0) $$We want to prove that both definitions produce the same result for any list of natural numbers:
$$ \forall xs : \text{List}(\mathbb{N}),\ \text{sum}(xs) = \text{sumAcc}(xs) $$This is proven by structural induction on the list xs.
Base case:
$$ \text{sum}([]) = 0 $$ $$ \text{sumAcc}([]) = \text{go}([], 0) = 0 $$Inductive step: Assume the inductive hypothesis:
$$ \text{sum}(xs) = \text{sumAcc}(xs) $$We want to prove it holds for x :: xs:
By the inductive hypothesis:
$$ \text{sum}(xs) = \text{sumAcc}(xs) $$So we substitute:
$$ x + \text{sum}(xs) = x + \text{sumAcc}(xs) $$And from the definition of go, we know:
Thus:
$$ \text{sum}(x :: xs) = \text{sumAcc}(x :: xs) $$Therefore, by induction, the optimized version sumAcc is provably equivalent to the original sum for all input lists:
This proof ensures that the tail-recursive version retains the exact semantics of the original function—guaranteeing correctness even after performance optimization. It’s a clear example of how Lean can verify low-level loop transformations that might otherwise introduce subtle bugs in traditional systems code.
So all this hurts my head. I’m glad that software is going to do this kinda thing, and a bit in awe of the brilliance of folks who build these tools.
As software complexity grows, formal verification tools like Lean are not merely nice to have—they become essential. Companies and research institutions increasingly adopt Lean to ensure high-quality, reliable code, making Lean skills highly valuable.
Conclusion
Lean isn’t just another programming tool; it’s a powerful ally in your pursuit of correctness and reliability in mathematics and software development. Whether you’re proving intricate mathematical theorems or ensuring your software meets precise specifications, Lean is a valuable skill that promises to shape the future of reliable software and mathematics. And yes, this all complicated, but it’s super powerful, and these are exactly the powers needed as we go into a world with vibe coding, power tools and fully automated build environments. Watch this space.
Stephen Carr
April 13, 2025 at 11:03 am
Really cool breakdown—love how Lean handles the base case and inductive step so cleanly. The simp tactic is slick